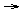< F-ARG1, F-PRED >
(As in The Evolutionary Emergence of Language: Social
function and the origins of linguistic form, edited by C. Knight,
M. Studdert-Kennedy and J. Hurford, Cambridge University Press. (2000) Pp.324-352.
Note: This HTML version may differ slightly from the printed
version; the printed version is the ``authorized'' version.)
This study1 focusses on the emergence and preservation of linguistic generalizations in a community. Generalizations originate in the innate capacities of individuals for language acquisition and invention. The cycle of language transmission through individual competences (I-languages) and public performance (E-language) selects differentially among innately available types of generalization. Thus, certain types of general pattern tend to survive in the community's language system as a consequence of social transmission.
Computational simulations are described in which a population that initially shares no common signalling system converges over time on a coordinated system. For the emergence of shared vocabularies, the dynamics of such systems are now well understood. (See, for example, Oliphant, 1997; Steels, 1996a, 1996b, 1996c, 1997)
This paper demonstrates how systems with syntax can emerge from the same fundamental population dynamics.
The essential ingredients of the computational model are:
This model incorporates no Darwinian selection of individuals by fitness, and no selection of meaning-form pairings by utility or psycholinguistic complexity. Although these classical evolutionary factors are relevant to the evolution of language(s), this paper attempts to abstract away from them in an attempt to discover what contribution may be expected from the purely mathematical workings of any system of social transmission with the four properties listed.
In such models, the language acquirer is also, in the early stages of the process, a language creator; and in the later stages of the process, when the population has converged to a common system, the language acquirer is a language maintainer.
The work described here draws from, and builds upon, work by Batali (1998) and Kirby (this volume).
The take-home conclusion of this paper is that general rules emerge and survive in the Arena of Use. This conclusion is argued on the assumption that a language has a two-stage life-cycle. In its history, a language exists in, and passes through individual brains, as grammars, or `I-language' (internalized language), and through communities, as utterances and their interpretations, or `E-language' (externalized language). The Arena of Use is where E-language exists2.
Rules are acquired by speakers of a language, on the basis of exposure to utterances of the preceding generation. Learners have dispositions to make certain generalizations, and not to make other logically conceivable generalizations, over the data they observe. Naturally, the common generalizing tendencies of language acquirers affect the shape of the language as it is transmitted from one generation to the next. But factors outside individuals' heads also influence the differential conservation of general patterns in the continuing language. A learner might have no innate preference between rival generalizations that are equally possible from the observed evidence, and might choose at random between alternative rules expressing these different generalizations. But such generalizations, although equally available to an acquirer, can have disproportionate consequences in the acquirer's eventual adult performance.
There are degrees of generalization. `Any odd number above 2 can be expressed by the morpheme X' and `Any prime number above 2 can be expressed by the morpheme X' are both generalizations about numbers, but the former is more general, in that it covers more numbers than the latter. If a child were given limited data compatible with either generalization, she might choose either. A learner who internalized the `odd' generalization would, as an adult, be likely to produce some meaning-form pairs not covered by the `prime' generalization, so that the `odd' generalization would be more likely to be the one made by successive generations. A learner who happened to make the `prime' generalization would use X for prime numbers and would use (or invent) a morpheme (or morphemes) other than X for non-prime odd numbers. If all numbers are equally likely to be expressed, there will necessarily be more exemplars in the Arena of Use of the `odd' generalization than of the `prime' generalization.
The generalizations that a learner acquires (i.e. the individual's grammar rules) determine the output performance data which will be the basis of the next generation's acquisition. Generalizations which give rise to larger proportions of the linguistic data in the Arena of Use will be better represented in the next generation's input. Thus the basic mechanism of language transmission itself will tend to favour patterns conforming to generalizations which embrace greater numbers of examples.
The examples just given depend on a subset relation between sets of potential meanings. All other things being equal, generalizations over supersets will be more likely to be perpetuated in the historically transmitted language than generalizations over subsets. (Prime numbers (over 2) are a subset of odd numbers (over 2).) In addition to such formal factors, external factors (for example, sheer usefulness, or conventions associated with common social interactions) can also influence the relative frequencies of linguistic data items. A generalization which happens to cover examples which are more frequent has a boosted likelihood of being propagated into the next generation.
The method for exploring the coherence and scope of these ideas is computer modelling of the evolution of simple languages in a community. The framework of these computer models is described below.
The simulated communities start with no language at all. What permits a shared communication system to `get off the ground' is the inventive capacity of individuals. Each individual is simultaneously a potential speaker/inventor and hearer/acquirer. The process of invention is computationally modelled by allowing speakers, when they are `prompted' to express some meaning for which they have not learnt any corresponding signal, to select a signal at random3 from a predefined, potentially infinite, set of forms. The process of invention cannot go beyond the bounds of the innately specified set of possible meaning-form mappings. For any given simulation experiment, there is a limited set of innately permitted types of mapping between meanings and forms. The innately specified possibilities for meaning-form pairings were experimentally manipulated in this work, in order to explore the contribution that innate dispositions and constraints impose on the structure of the language that eventually emerges in the community.
It is also assumed that speaking/invention and hearing/acquisition are parallel applications of the same principles of language use. The central assumption about language use is that the processes of speaking and hearing both call upon the same internalized declarative mappings between meanings and forms, i.e. competence grammars. These mappings can take the simple form of lexicons, in which atomic meanings are paired with atomic forms, in a list. Or, more complexly and realistically, the meaning-form relations can also be partly specified by compositional rules, stating that particular configurations of forms have complex meanings which are a function of the meanings of the constituent forms and the particular shape of the construction containing them. The meaning-form pairings that can be specified by such compositional rules are defined and constrained in various experimental ways in this study.
More specifically, a speaker who has already learned a pairing between a particular atomic meaning and a particular form (i.e. internalized a lexical entry), would, if prompted to express this meaning, simply look up the meaning and `speak' the corresponding form. If the speaker is prompted with an atomic meaning for which it has no lexical entry, it speaks a form randomly selected from a large predefined set of possible syllables. This invention process is genuinely random, and in no way guided by the grammars or behaviour of other individuals in the community. Inventors make no effort to invent forms consistent with existing usage.
If a speaker is prompted to express a complex (i.e. non-atomic) meaning, there are again two possibilities. If the speaker has already learned a rule mapping this general type of meaning onto either a specific form or a general type of form, the rule would be applied, and the appropriate form would be spoken. But if the speaker has learned no such rule, then again invention is invoked, and the speaker either (a) speaks a random atomic syllable or (b) selects at random from a specified set of general rules mapping complex meaning-types compositionally onto corresponding form-configurations, and follows that rule to speak a particular form, a string of syllables. In the latter case, following the rule involves, recursively, a prompt call to express the meanings which are subparts of the original complex meaning. The probabilities with which options (a) and (b) here are followed are varied experimentally.
Rule-learning is only associated with the act of hearing. Inventors do not learn from their own inventions. That is, after inventively selecting a random syllable, or string of syllables, to express some meaning, the inventor does not `learn from herself' and internalize a corresponding rule. Thus a speaker/inventor would, if prompted with the same meaning on several occasions, almost certainly invent different forms for it. The diversity thus created is something for hearers/learners to cope with.
Turning now to the behaviour of hearer/acquirers, learners acquire their grammars on the basis of positive information only. An individual who has already learned a pairing between a particular atomic meaning and a particular form would, on observing this same meaning-form pairing used by another speaker, simply do nothing. If, however, the hearer, while in the learning phase of its life, observes a novel atomic meaning-form pair, this new pair is added to the hearer's lexicon. If a hearer/learner observes the use by another speaker of a particular complex meaning paired with a particular form, then either (a) a `brute' rule is acquired relating this meaning to this form, or (b) the hearer structures the parts of the meaning in some permitted way, consistent with the given meaning-form pair, and acquires a general rule relating this meaning-type to this form-type, and applies the hearing/learning procedures, recursively, to the parts. Again, the probabilities with which options (a) and (b) here are followed are varied experimentally. There is no sense in which a learner's growing knowledge is evaluated against any `target grammar'.
Several more technical assumptions are made about the ways in which speakers and hearers make use of their internalized gramars or rule-sets. Firstly, it is assumed that acquired rules take precedence over `innate' dispositions. This was implicit in the paragraphs above, in that invention on the part of a speaker, or learning on the part of a hearer, is only called upon where the individual does not already possess a rule specifying the relevant meaning-form pair. A second assumption is that earlier acquired rules take precedence over later acquired rules. This embodies in a very simple way the principle that speakers' uses are roughly influenced by the frequency with which they observe meaning-form pairings. If a particular meaning-form pairing is more widespread in the community than some other, the likelihood is that the more frequent pairing will be observed earlier by a learner.
The simulated agents can talk to each other about a little universe, borrowed from Cann's (1993) semantics textbook. This universe includes some people (Fiona, Bertie, Ethel, Jo), a cat (Prudence), and a dog (Chester). These individuals can have properties such as being happy, running or singing; and they can be in dyadic relationships, such as liking, or loathing, with each other. They can participate in the triadic relationship of giving (the humans can give the animals to each other). So far, this is within the bounds of first order predicate logic; but the simulation also allows embedding of a proposition as second argument of the 2-place predicate SAY (whose first argument must be human). This embedding is recursive, up to an arbitrary limit. The simulation does not deal with logical quantification.
Here is a list of some possible messages.
These are in a simple predicate-argument format.
HAPPY(FIONA)
LIKE(FIONA,BERTIE)
LOATHE(BERTIE,FIONA)
GIVE(ETHEL,BERTIE,CHESTER)
SAY(JO,(HAPPY(FIONA))
SAY(ETHEL,(GIVE(JO,BERTIE,PRUDENCE)))
SAY(BERTIE,(SAY(FIONA,(RUN(ETHEL))))
The simulated speakers and hearers are not themselves members of the little universe about which they exchange messages. (Thus Fiona, Chester et al. are like the community's gods, ever present and ever talked about.)
The meanings which simulated individuals could be prompted to express
ranged from atomic `concepts', such as FIONA, LOATHE or
GIVE, to complex propositions, such as
SAY(FIONA,(GIVE(BERTIE,JO,CHESTER))).
The simplest kind of rule that a learner can acquire is a lexical entry
specifying a pairing of an atomic meaning with a single syllable,
represented as a number. For
example:
WEALTHY : vom
JO : tot
SAY : bit
It is also possible for a learner to acquire a rule linking a whole
proposition with a single syllable. For example:
WEALTHY(BERTIE) : gaq
SAY(FIONA,(HAPPY(CHESTER))) : lih
LOATHE(CHESTER, PRUDENCE) : mis
For the first three experiments described below, there was
also a single type of rule for expressing whole propositions in a
compositional way, by specifying a particular ordering of
sub-expressions corresponding to the meanings of the parts of the whole
proposition4. An example of such a rule, for a
1-place predication, is:
PRED(ARG1) 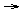< F-ARG1, F-PRED >
This translates as ``To express a proposition consisting of a 1-place
predicate and a single argument, use a string consisting of the form for the
argument, followed by the form for the predicate. Another example is:
PRED(ARG1,ARG2,ARG3) 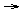< F-ARG3, F-PRED, F-ARG1, F-ARG2 >
This translates as ``To express a proposition consisting of a 3-place predicate and three arguments, use a string consisting of (1) the form for the third argument, (2) the form for the predicate, (3) the form for the first argument, and (4) the form for the second argument.''
Such rules are essentially constituent-ordering rules, i.e. rules for ordering the forms which express predicates and their arguments. There are two different ways of ordering a predicate-form and a single argument-form, six different ways of ordering a predicate-form and two argument-forms, and so on. Note that such rules contain no autonomous syntactic categories, being simply `translation rules' from semantic representations to `phonetic' representations. I do not believe that natural languages in fact manage without such autonomous syntactic categories in (at least some of) their rules; the present treatment is clearly a simplification.
Note that there are two ways of expressing a whole proposition, either compositionally as a string of expressions for the constituent meanings, or noncompositionally (holistically5) as a single syllable. The compositional method is in a clear sense more general than the holistic method. Rules of the compositional sort use variables over the meaning constituents and the corresponding elements in the output syllable-string. Such a rule will apply to any proposition with the appropriate number of arguments. A holistic rule, on the other hand, is completely specific, applying to just one particular proposition, e.g. LIKE(FIONA,BERTIE). We will see that the cyclic process of production and acquisition over many generations favours the perpetuation of the more general type of rule, at the expense of the more specific type of rule.
An inventor who produces a syllable-string corresponding to some given propositional meaning, for which she previously had no rule, chooses at random an arbitrary ordering of the constituents of the given meaning, and then expresses the meaning-constituents in the order chosen. In some cases, this second round of meaning-expression may be straightforward, simply involving lexical lookup of the expressions to be used for the constituent meanings. In more complex cases, the speaker/inventor may have no existing rule for expressing some of the constituent meanings, and in such cases further calls to the invention procedure are made. In sum, an inventor, prompted to express a proposition (and not taking the simple single-syllable option), goes through the following operations:
In an extreme case, a speaker/inventor prompted to express some complex proposition, could utter a long string of syllables, each one invented, in an invented order.
As an example of speaking involving some rule-invention, suppose that a
speaker has only the following rules:
WEALTHY : vom
JO : tot
SAY : bit
PRED(ARG1) 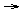< F-ARG1, F-PRED >
Now, this speaker is prompted to express the meaning:
SAY(FIONA,(WEALTHY(JO)))
The top-level proposition here is a 2-place predication, with the
predicate SAY, first argument FIONA, and second argument the
proposition WEALTHY(JO). The speaker has no rule for expressing a
2-place predication, and so must invent one. The speaker picks a random
ordering of the three constituents, let us say the `SOV' order <
FIONA, (WEALTHY(JO)), SAY >. Now the speaker
is prompted to express each of these constituent meanings in the order
chosen. The first is FIONA; the speaker has no expression for
FIONA and must therefore invent one. Let's say she picks the
random syllable kuf. Moving on now to the second meaning-constituent,
the proposition (WEALTHY(JO)), the speaker already has a rule
(above) for expressing such 1-place predications; this rule calls for
the expression of the single argument to precede the expression of the
predicate. Accordingly, the speaker is prompted to express JO.
She has a rule for JO, which is expressed as the syllable tot.
She also has a rule for the predicate WEALTHY, specifying the
syllable vom. All that remains is to express the predicate SAY,
for which there happens also to be an existing rule, specifying the
syllable bit. In sum, the outcome of this process is that the speaker
utters the string of syllables:
< kuf, < tot, vom >, bit >
The output syllable-strings in these simulations retain any bracketing inherited from the nesting of propositions inside each other in the meaning-representations. Thus, in these simulations, the embedding structure, but not the linear order, of an expression for a complex meaning is derived from the embedding structure of the complex meaning itself. This bracketing is available to the simulated hearer/acquirers. Undoubtedly, there are both realistic and unrealistic aspects to this treatment. In natural languages, syntactic clause embedding tends to reflect the embedding of propositions at the semantic level. On the other hand, clearly, hearers do not receive completely explicit signals of bracketing. In further work, it will be interesting to remove these brackets and implement a full string-parsing mechanism in hearers, which could conceivably give rise to bracketings other than those present in the original meaning-representation. In the fourth experiment described below, the bracketing of the output string did not correspond exactly to that of the input meaning-representation.
When a speaker/inventor uses some new forms in an utterance, she does not remember them. But the hearer/acquirer who observes the meaning-form pair generated by the speaker/inventor can acquire the rules which were used in generating it. A simple case of acquisition would involve a single lexical item. Say, for example, a hearer observes a speaker uttering the syllable jam for the atomic meaning BERTIE. If the hearer did not already have a lexical entry linking this syllable to this meaning, she would acquire it. Likewise, if a hearer hears for the first time a single syllable used to express a complex meaning, say LOATHE(BERTIE,CHESTER), she would acquire a rule linking this complex meaning to the observed syllable. The case of acquiring an ordering rule is somewhat more complex, but follows the same principles as were explained above for the case of rule-invention. An example follows.
Suppose the hearer has only the following lexical entries:
WEALTHY : vom
JO : tot
This hearer has not yet any general rules for expressing propositions.
She observes a speaker producing the meaning-form pair:
WEALTHY(JO) : < vom, tot >
In this example, as it happens, the expression for the predicate precedes
the expression for its argument. The hearer/acquirer notes that this is
the order of elements which has been used, and accordingly internalizes
the general rule:
PRED(ARG1) 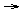< F-PRED, F-ARG1 >
The hearer/acquirer generalizes a constituent-ordering rule on the basis of a single exemplar.
Whereas in the speaking/invention process it is possible for a particular
production to involve more than one invention, in the
hearing/acquisition process, a limit of one rule acquisition per
observation is applied. Thus, it is not possible to learn a general
rule for a construction and a number of the lexical entries involved
all at the same time. This has the effect of imposing a typical bottom-up
ordering on the language-acquisition process. A learner learns atomic
lexical correspondences before learning constructions, as in the example
just given. It is, however, possible for a learner to acquire a new
atomic lexical entry after the acquisition of a construction in which it
is used. For example, the hearer/learner in the above example might
next observe the meaning-form pair:
WEALTHY(FIONA) : < vom, but >
Having already acquired both a lexical entry for WEALTHY and a rule
stating how 1-place predications are expressed, the hearer can acquire
the next lexical entry:
FIONA : but
The simulation program ran repeatedly through the following steps,
starting with a `blank' population consisting of some adults and some
children.
Repeat
This model of population turnover, with speaking and learning, is essentially similar to both Kirby's (this volume) and Batali's (in press).
In all the experiments reported below, there were, at any given time, four adult speaker/inventors and one child hearer/learner6. These numbers are unrealistically small, of course, but they made for fast runs. Some experiments with larger populations were carried out, and these converged more slowly on results essentially similar to those reported below, so there is no reason to believe that the general conclusions would be different, given larger populations.
Within the framework sketched above, four experiments were carried out, progressing from the illustration of quite simple principles to the exploration of slightly more complex cases.
As noted, the community started with no language at all. The speakers in the first generation had not themselves gone through a language-learning experience, and therefore, when prompted to express any particular meaning, always had to resort to invention. The hearer/acquirer was thus presented with an uncoordinated jumble of randomly invented meaning-form pairs. Speakers were prompted to express atomic meanings (e.g. BERTIE, or SAY or GIVE) 50% of the time, and simple or complex whole propositions (e.g. HAPPY(CHESTER) or , LIKE(JO,PRUDENCE) or SAY(BERTIE,(HAPPY(JO)) ) 50% of the time.
Given an atomic meaning, the inventor would select a possible syllable at random. Given a complex meaning (i.e. a whole proposition), the inventor would select a random syllable (for the whole meaning) 50% of the time, and otherwise would select a rule at random for expressing the particular type of meaning involved, by the process explained above.
At an early stage in this simulation (after 2 cycles), a typical individual had nothing more than a big lexicon, for both simple and complex meanings. There were no general syntactic rules. There was multiple synonymy. Given below is a subset of such a typical individual's grammar.
|
EXPERIMENT 1:
WEALTHY : lar |
At a later stage, after 15 cycles, a typical speaker had adequate productive syntactic rules for the domain, some complex meanings were still looked up lexically, and there was still some synonymy, as shown next.
|
EXPERIMENT 1:
PRED(ARG1)
SAY : feq |
Finally, after 30 cycles, a typical speaker had a maximally economical grammar7 for this domain, with three adequate general syntactic rules, no `idiomatic' rules expressing whole propositions as lecical items, and no redundancy (synonymy) in the lexicon, as shown next.
|
EXPERIMENT 1:
PRED(ARG1) |
Several things are shown in this experiment: social coordination, the elimination of synonymy, and the take-over by general rules.
Social coordination At first, when no speaker has any learned meaning-form correspondences, such correspondences are randomly invented in a way that is not coordinated across the community. Thus the first hearer/acquirers hear a variety of different meaning-form correspondences, and they hear them with differing frequency. Hearer/acquirers do not, however, hear all possible forms corresponding to a given meaning (because, of course, not all possible meaning-form correspondences have been invented by the first generation). So, even in the second generation, there is a limited set of meaning-form correspondences circulating in the community. Hearer/acquirers in these simulations are affected by the frequency with which they have experienced particular meaning-form pairs. They internalize (i.e. acquire) all observed meaning-form pairings, but in their own spoken performance will only utter the form which they acquired first for a particular meaning, which was likely to have been one of the more frequent forms for that meaning in circulation. In this way, the set of form-meaning correspondences in circulation in the community is gradually reduced, resulting in a shared set across all members of the community.
Elimination of synonymy It will be evident that the process just discussed also leads to the elimination of synonymy. If a speaker has several forms corresponding to one meaning, but only actually uses one of them when speaking, the next generation will only hear a single form for that meaning from this speaker. Taken together with the social coordination just discussed, this clearly results in the elimination of synonymy from the community's language.
Comparing the two mini-grammars in the two last tables above, note that the ``later'' speaker's and the ``final'' speaker's respective grammars had different rules for the expression of 3-place predications. This reflects and illustrates the random origin of the rules. Which of the 24 possible 3-place predication rules comes out on top is a matter of chance, as equally valid alternative forms die out (with their individual owners) and the population converges on the only remaining form.
Generality of syntactic rules Early generations of speakers in these simulations acquired idiosyncratic, noncompositional rules for particular whole propositions. Speakers in the final stages of the simulations only acquired general syntactic rules, each applying to a whole class of propositions (1-place, 2-place, 3-place). This is also a consequence of the social coordination taking place in the simulated community. The first generation of speaker/inventors invent various different constituent orders for expressing the propositions they are prompted to express. They invent inconsistently, even within individuals. For instance, a speaker prompted with LOATHE(BERTIE,FIONA) might invent an `SVO' ordering for it, but later, when prompted for another (or even the same!) 2-place predication, might invent a `VOS' ordering for it. At this stage, too, the community will not have settled on a coordinated vocabulary for the basic predicate and argument terms.
A hearer/acquirer can only acquire one rule at a time from any particular observation of a meaning-form pair. In early stages of the simulation, then, it is likely that the observed meaning-form pairs will have inconsistent constituent ordering and also use unfamiliar (i.e. not yet acquired) lexical items. At this stage, because of the limitation to acquiring only one rule per observation, acquirers cannot decompose an observed string into elements corresponding to constituents of the simultaneously observed meaning. For instance, a hearer/acquirer might be given the meaning LOATHE(BERTIE,FIONA) and the syllable string < gem, duc, mix >. At an early stage, the learner is unlikely to have acquired lexical entries linking any of these particular meanings with any of these particular forms, and will not be able to make any generalization about the ordering of form-elements corresponding to elements of the proposition. In this circumstance, no learning occurs.
As the meaning-form pairs used by speakers may consist of simple term-syllable correspondences (e.g. ETHEL : faf), acquirers after a few generations will begin to acquire a coordinated basic vocabulary. Given such a stock of basic vocabulary items, it will now be possible for hearer/acquirers to acquire the constituent-ordering rules that they are able to generalize from their observation of string-proposition pairs. For instance, now a hearer is likely to have acquired, say, the lexical pairings LOATHE:duc, BERTIE:gem, and FIONA:mix. If the hearer/acquirer now observes the complex pair LOATHE(BERTIE,FIONA):< gem, duc, mix >, she will be able to infer the general rule that 2-place predications are expressed in `SVO' order.
An individual who has acquired a general rule will be prompted, as a speaker, to express a variety of propositions. For some of these propositions, the speaker may happen to have, and may use, an idiosyncratic, holistic rule. But for other propositions, the speaker will have no such idiosyncratic rule; if such a speaker has a general rule for expressing all propositions of that type (e.g. 2-place), it will be used. For the cases where the general rule is applied, the community of learners in the next generation will be presented with a consistent set of exemplars. There will thus be an increasing tendency, as the simulation progresses, for speakers to converge on a common set of meaning-form patterns.
In the previous experiment, we saw how idiosyncratic, holistic meaning-form pairings are eliminated from the community language in favour of general rules. This was an effect of the greater generality of general (i.e. non-holistic) rules. By definition, a general rule applies to a larger proportion of the meaning-space than a single holistic rule. In all the experiments described here, the meaning-space was restricted for practical purposes, by arbitrarily limiting the depth of recursion, to 4137 possible meanings. In the first experiment (and in the third and fourth) these meanings were roughly equi-probable, but it is possible to manipulate the meaning space in such a way that a particular meaning occupies a disproportionate share of it. If some particular meaning is expressed with greatly enhanced frequency in the community, we can expect an original holistic form-meaning pairing to persist in the language, regardless of the existence, alongside it, of general rules which could also be used to express this meaning. This is indeed what happens in these simulations, as shown in the current experiment.
In this second experiment, speakers ``choose'' to express a particular meaning, SAY(JO,(HAPPY,FIONA)), with artificially high probability. In this case, a grammar with three general syntactic rules, plus one idiomatic rule for the particularly frequent meaning emerges, as shown below.
|
EXPERIMENT 2:
PRED(ARG1)
|
Because of the artificially inflated frequency of one proposition, a learner is likely to acquire the idiosyncratic rule involving it before acquiring the two general rules required to express this meaning in a regular way.
Given the meaning-space used in these simulations, it was possible to identify a critical frequency band above which a proposition tended to retain an idiomatic, holistic expression. Runs were carried out with the probability of the meaning SAY(JO,(HAPPY(FIONA))) being expressed set at various values between 0.01 and 0.09. That is, on an arbitrary occasion of a speaker being prompted to express some meaning, the probability of that meaning being SAY(JO,(HAPPY(FIONA))) would have been, say, 0.03, and the probability of the speaker being prompted for any other meaning in the meaning-space was, accordingly in this case, 0.97. These results are shown in a graph in Figure 1.
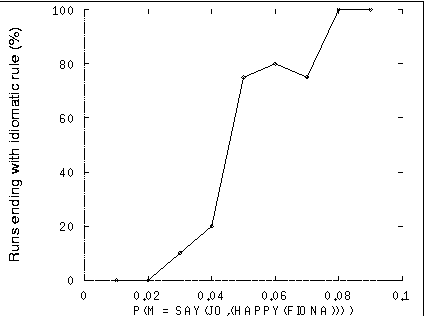
Figure 1. These runs showed that when the frequency of the prompt for the
meaning SAY(JO,(HAPPY(FIONA))) was 2% or below of all
meaning-prompts, this meaning was not expressed idiomatically. When the
frequency of the prompt for this meaning was 8% or above, it was always
expressed idiomatically. Between 2% and 8%, results were mixed, with
idiomatic expression tending to increase with frequency.
The previous experiments have shown the emergence of languages conforming to generalizations that the language-acquirers are disposed to make. In these experiments, acquirers had a strong disposition to generalize from observation. That is, if an acquirer could assimilate a particular observed meaning-form pair at the `cost' of internalizing just one general rule, then that general rule would immediately become part of the acquirer's grammar. This can be seen as a strong influence of innate language-forming dispositions on the emerging shape of the community's language. In the next experiment, it will be shown that if individual acquirers' dispositions are considerably weakened, then, although the individuals' grammars will contain many non-general rules, nevertheless the common E-language shared by the community is shaped to conform to a small set of general rules.
In this experiment, acquirers were disposed to generalize from experience (i.e. to induce general rules) with a probability of only 0.25. Otherwise, acquirers simply rote-memorized the form-meaning correspondences they experienced. The resulting internalized grammars are redundant --- see below. The emergent community E-language generated by such redundant grammars can be described fully by the general rules and the lexicon, without use of the redundant idiosyncratic rules. That is, all the idiosyncratic rote-learnt correspondences conform to the general rules anyway. Some acquirers even acquire no general rules at all, but their rote-learnt sequences still conform to the rule-generated community language.
|
EXPERIMENT 3:
GENERAL RULES
ROTE-LEARNT CORRESPONDENCES HAPPY(CHESTER) : < qot, soy > RUN(CHESTER) : < qot, fur > GIVE(JO,JO,BERTIE) : < xiy, qaq, qaq, sud > GIVE(JO,ETHEL,PRUDENCE : < xiy, qaq, lef, lef > SAY(JO,(HAPPY(FIONA))) : < qaq, < def, soy > , xuh > SAY(JO,(LOATHE(FIONA,CHESTER))) : < qaq, < def, qot, qow > , xuh > SAY(ETHEL,(LIKE(FIONA,FIONA))) : < lef, < def, def, hoc > , xuh > SAY(BERTIE,(GIVE(ETHEL,CHESTER,BERTIE))) : < sud, < xiy, lef, qot, sud > , xuh > SAY(FIONA,(GIVE(ETHEL,FIONA,BERTIE))) : < def, < xiy, lef, def, sud > , xuh > SAY(FIONA,(SAY(JO,(LOATHE(JO,FIONA))))) : < def, < qaq, < qaq, def, qow > , xuh >, xuh > SAY(JO,(SAY(JO,(LOATHE(BERTIE,FIONA))))) : < qaq, < qaq, < sud, def, qow > , xuh > , xuh > SAY(FIONA,(SAY(BERTIE,(GIVE(JO,ETHEL,CHESTER))))) : < def, < sud, < xiy, qaq, lef, qot > , xuh > , xuh >
|
We have become accustomed, in the Chomskyan era, to assuming that regularities observed in the language behaviour of a community will be represented economically, as regularities, in speakers' heads. And, further, we have assumed that it is the regularities in speakers' heads that in fact determine the regular observed behaviour. This experiment shows (again) the reverse effect, the effect of social coordination on the grammars of individuals. The individuals in this experiment all internalized many non-general rules, rote-learnt facts about particular meaning-form pairs. But these holistically memorized meaning-form pairs all conformed to the general constituent-ordering rules which had become established in the community as a result of a quite weak (25%) tendency to generalize from observation. If `the language' is taken to be the abstract system, described in the most economical way, apparent in the behaviour (including intuitive judgements of form-meaning correspondence) of the community, we are dealing with E-language. The economizing generalizations made by the descriptive linguist are, then, statements about the E-language, and not about any individual's I-language.
The grammars arrived at in the three previous experiments missed a kind of generalization that one normally finds in real languages. These simple grammars all had three separate general rules for each of the three types of predication, 1-place, 2-place, and 3-place. In natural languages, of course, one typically finds consistent constituent-orders for intransitive, monotransitive and ditransitive clauses. The previous experiments reached these unnatural grammars because the generalizing principles available to speaker/inventors and hearer/acquirers were limited to generalizations over constituent-order based on the elements of the given meaning-representations. For example, an inventor inventing a rule to express a 2-place predication shuffled the three terms involved (PRED, ARG1, ARG2) into some random order. In parallel, all that an acquirer noted when internalizing a general rule on the basis of an observation was the order of the constituents. This ordering was the only permitted operation on meaning-representations. There was no linkage between the orderings `chosen' for 1-place, 2-place and 3-place predications.
In the final experiment, speaker/inventors and hearer/acquirers were allowed a further operation on meaning-representations, namely restructuring into binary bracketed structures. For example,
LOATHE(BERTIE,FIONA)
would be restructured as
[LOATHE, [BERTIE, FIONA] ].
And
GIVE(JO,CHESTER,BERTIE)
would be restructured as
[GIVE, [JO, [CHESTER, BERTIE] ] ].
The restructuring operation thus reduced all meaning-representations (1-place, 2-place, 3-place) to uniformly binary (often recursively nested) structures. Such binary structures could be input to the same (re)ordering and lexical lookup operations as were used by speaker/inventors and hearer/acquirers in the previous experiments.
The binary restructuring rule can apply to predications of any degree (1-place, 2-place, 3-place), and so is more general than any of the `semi-general' rules we have seen emerging in the previous experiments.
In this experiment, individuals were permitted to invent/learn either (a) semi-general rules for each type of proposition (1-place, 2-place, 3-place), as before, or (b) to break any proposition into a binary branching structure, and invent/learn a general rule for expressing any such binary branching structure. The (a) and (b) possibilities here were chosen at random on each occasion of use, but with equal probability.
In this experiment, instead of three separate rules for 1-place, 2-place and 3-place predications, the community converged on a language in which all types of propositions were expressed with uniformly right-branching binary structures. The internalized binary restructuring rule cannot be represented in the same format as the constituent-ordering rules given in the grammars of previous experiments, and so will not be given here (in fact, of course, it was piece of computer code). Rather, a set of example sentences produced in the evolved community language will be given, along with the lexicon of the language.
|
EXPERIMENT 4:
LEXICON SOME EXAMPLE SENTENCES
|
The single binary rule covers more data than any of the semi-general rules specific to particular degrees of predication. The less productive rules were permitted throughout to speakers/inventors and hearers/acquirers, and were indeed present earlier in the simulation. But they were superseded by the single more general binary-structure-inducing rule.
(The fact that this particular run of the experiment ended with right-branching, rather than left-branching, structures is not significant. It was an artifact of this particular implementation, deriving from an `innate' behaviour of the individuals, who `discovered' right-branching structures before happening on left-branching ones.)
In brief, the four experiments have shown:
The model used here incorporates neither Darwinian natural selection nor rewards for successful communication. Throughout a given experiment, the generalizing dispositions attributed to individuals remain constant. And although the individuals speak and hear, there is no modelling of real communication, since the hearers are always given both the full form and the full meaning for the form-meaning pairs uttered by speakers. A more sophisticated simulation would attempt to model the co-evolution of innate generalizing dispositions and languages as cultural objects created, transmitted and maintained by communities.
It has been shown here that more general linguistic rules are favoured by a completely non-biological mechanism, namely the social transmission of language from one generation to the next. But this does not mean that natural selection is necessarily neutral with regard to degrees of linguistic generalization. To the extent that the social process leads to grammars with particular types of generalizations, there will be evolutionary pressure to produce individuals capable of acquiring such grammars with facility. In a co-evolutionary scenario, the individuals' innate, biologically determined, dispositions to make certain kinds of linguistic generalization are the source of the learning behaviours from which the social transmission process selects to produce communal grammars of greater generalization. But in turn, the evolved more general communal grammars provide a human-made environment which selects for individuals with greater aptitude for learning just such languages8.
What are the limits to the kind of generality towards which languages will apparently tend, according to the tendencies shown in these experiments? The kinds of generalization attributed to speaker/inventors and hearer/acquirers in this study have all been relatively sensible. More extreme and far less sensible kinds of generalization are theoretically possible. For example, on hearing a particular syllable used to express a particular atomic meaning, an acquirer might in theory make the absurd overgeneralization that any syllable can be used to express any meaning. Human learners don't do that --- why not?
Any tendency to make overgeneralizations of such an absurd kind would presumably be eliminated by natural selection based on success in correctly divining a speaker's meaning and/or successfully signalling ones own meaning. Any mutant displaying any tendency to generalize from the primary linguistic data in ways which will lead to her being misunderstood, as she would be if she used any form to convey any meaning, will be at a disadvantage.
I will give here a few brief notes on the more significant differences between the simulations reported here and similar current work by Kirby (this volume) and Batali (in press). (A much fuller survey and comparison of models of this general type is to be found in Hurford (in press).)
Compositionality Kirby's model claims to explain the emergence of compositionality in language. In my model, the availability of compositional principles is assumed. This is apparent in both the invention and the acquisition behaviours. The essence of compositionality in a broad sense is not peculiar to language. Any deliberate behaviour that can be analyzed into parts will work according to the principle that the outcome of the whole behaviour is a function of the separate outcomes of the parts of the behaviour. For example, the chimpanzee behaviour of picking up a stick, breaking it to an appropriate length, inserting it into an anthill, withdrawing it, and licking off the ants depends for its overall success on the success of each constituent action. Vision certainly works on a compositional principle, with a complex picture being built up from a host of sensory inputs. (This is not to deny the existence of some differences between the compositionality of language and of other behaviours.)
Speed The simulations reported here converge on coordinated languages with syntactic rules much faster than those described by Kirby (this volume) and Batali (in press). This is due to the far greater power attributed to individuals in this simulation, inherent especially in their invention capacity. The goal of this paper has been to show an effect of social transmission on the kinds of generalizations that may be hypothesized to be innately available to individuals. For this purpose, generalizations of a certain power had to be introduced, in order to be compared. Exactly what generalizations humans are in fact disposed to make in their language acquisition is an empirical matter.
From vocabulary to grammar: analysis vs. synthesis
Both these simulations and those of Kirby (this volume) go through an early stage of `one-word' communication. At this stage, speakers have no general grammar rules, but only lexical items.
In Kirby's model, at the one-word stage, the single utterances memorized by speakers express whole propositions. Kirby's simulation thus follows an `analytic' route from vocabulary to grammar. In the analytic route, preexisting unitary signals with conventionalized, but complex, meanings become decomposed into segments, to each of which is assigned some subpart of the original complex meaning; the decomposition and assignment of meaning is such that the (original) complex meaning is a function of the (new) meanings of the parts.
In my model, the early memorized utterances can also stand for atomic subparts of meanings, such as names and predicates. These simulations follow a `synthetic route from vocabulary to grammar. In the synthetic route, preexisting unitary signals with conventionalized meanings are concatenated into strings; these strings then become organized to convey meanings composed of the original meanings of the units.
It is not a priori obvious whether language evolution had to take just one of these routes, or whether it was a mosaic of both routes. See Wray (1998) for some relevant arguments.
Contrasting the empirical claims implicit in various possible formalisms which capture different types of generalization over linguistic data, Chomsky presents two sets of conceivable data over which generalizations of two different types are respectively possible: he numbers these examples (16) and (17), and writes of,
... the empirical hypothesis that regularities of the type exemplified in (16) are those found in natural languages, and are of the type that children learning a language will expect; whereas cyclic regularities of the type exemplified in (17), though perfectly genuine, abstractly, are not characteristic of natural language, are not of the type for which children will intuitively search in language materials, and are much more difficult for the language-learner to construct on the basis of scattered data. (Chomsky, 1965:43)
Note the strong implication that ``found in natural languages'' equates to ``what the language-learner will construct''. This paper accepts the contribution to the shape of languages made by the natural generalizing dispositions of language-learners. What this paper shows is that the mechanism of social transmission of language adds an extra filter, or selection principle, to the processes giving rise to the generalizations that are characteristic of natural languages.